Introduction to Antenna Engineering

Wireless Communication System

Friis Formula for Isotropic Sources

When I decrease transmitted power while perserving same system requirements like bitrate, SNR, Cost...etc we will not consider case of Near-far problem for design of cellular system in this case we are assuming we are having two antennas which are left alone in the space, also increasing transmitted power will not just affect battery but we will also be required to implement multiples of power amplifiers to increase transmitted power which will affect precedingly area of chip.
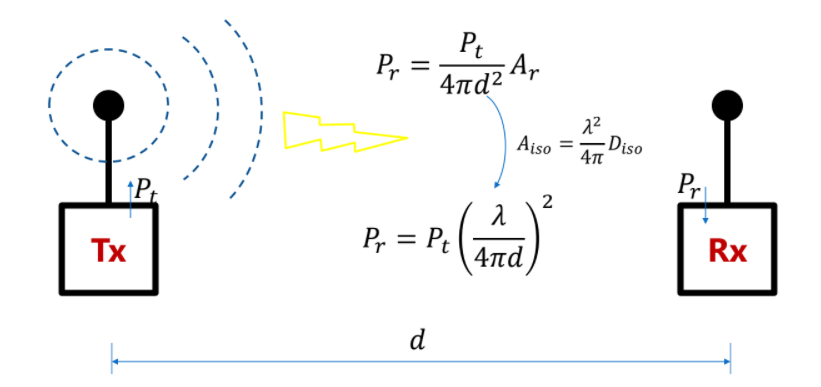
Isotropic antenna means an antenna that transmits all of its power in all directions but this will affect us alot as we are losing much power in many directions that we don't care about. $$P_r={{{P_t} \over {4 \pi d^2}}A_r},\space A_r: area of Reciever , \space P_t:transmitted power$$ because the antenna is Isotropic so it is transmitting radiations in form of spherical waves where the distance that it covers, is constrained by the diameter of the sphere \(d\) which is the distance betweem Transmitter \(T_x\) and Reciever \(R_x\)

Directivity

as we said before Isotropic distributes its power equally along all directions so, $$p_{iso}={P_{rad} \over {4 \pi r^2}}$$ $$Capital P: Total Power,\space Small P: Power Density$$ while normal radiating antenna distributes its power according to a certain spatial distribution that is \(f(\theta,\phi)\),then $$P_{rad}={{P_{iso} \over 4 \pi r^2}f(\theta,\phi)}$$ $$D_{iso}={{P_{rad}(\theta ,\phi)}\over P_{iso}}=f(\theta,\phi)$$ $$D_{iso}:Directivity \space of \space the \space Antenna$$ $$D_{dB}=10log(D_{iso})dB_i, \space i:means \space relative \space to \space isotropic$$ Effective area of Isotropic Antenna, \(D_{iso}=1\) $$A_{iso}={{\lambda^2} \over {4\pi}}D_{iso}={{\lambda^2} \over {4\pi}}$$ Recieving power when we substitute with effective area formula in friis formula $$P_r=P_t{({{\lambda}\over{4 \pi d}})^2}$$ this formula you will find it also in satellite communication course, this formula also determines link budget which indicates how much power i need to transmit to satisfy reciever sensitivity where reciever sensitivity can decrease when we increase the frequency of operation or increasing the distance between transmitter and reciever according to Friis Formula $$P_{r,dBm}=P_{t,dBm}+20log({{\lambda}\over{4 \pi d}})$$ $$then, P_{r,dBm}=P_{t,dBm}+20log({{c}\over{4 \pi d f}})$$ $$then, P_{r,dBm}=P_{t,dBm}-{[{20logf+20logd+{20log({4\pi \over c})}}]}$$ $$then, P_{r,dBm}=P_{t,dBm}-{[{20logf_{MHz}+20logd_{km}+{20log({4\pi \over c})}+20log{(10^6)}+20log{(10^3)}}]}$$ $$then, P_{r,dBm}=P_{t,dBm}-{[{20logf_{MHz}+20logd_{km}+{20log({4\pi \over c})}+180}]}$$ then, \(P_{r,dBm}=P_{t,dBm}-FSPL\), where \(FSPL\): Free Space Path Loss

Tx and Rx Directive Antennas

The antenna acts like a spatial filter as it redistributes radiation according to its directivity but making the antenna more directive affects beam width of the radiation it act like a ballon that we put on it a lot of pressure to make it like a pencil $$P_r={{P_tD_t}\over{4 \pi d^2}}A_r$$ $$A_r={{\lambda^2}\over 4\pi}D_r$$ $$P_{r,dBm}=EIRP_{dBm}+D_{r,dBi}-FSPL_{dB}$$ $$EIRP_{dBm}=P_{t,dBm}+D_{t,dBi}$$ EIRP===>Effective Isotropic Radiated Power which indicates how much power I need to transmit relative to directive source $$FSPL_{dB}=20logd_{km}+20logf_{MHz}+32.4$$ Notes on Spherical Co-ordinates\((r,\theta,\phi)\):
@\(r=constant\)==>sphere,@\(\theta=constant\)==>Cone, @\(\phi=constant\)==>Plane

$$P_r=P_t({\lambda \over {4\pi d}})^2D_tD_r$$ Now an important factor which is directivity gave us indication that we can increase reciever sensitivity by increasing directivity without increasing transmitted power. very small beam width requires very complex allignment for antenna to recieve the signal